本节书摘来自异步社区《Python极客项目编程 》一书中的第2章，第2.1节，作者 [美] Mahesh Venkitachalam，王海鹏 译，更多章节内容可以访问云栖社区“异步社区”公众号查看。

第2章 万花尺

我们可以用万花尺玩具（如图2-1所示）来绘制数学曲线。这种玩具由两个不同尺寸的塑料齿轮组成，一大一小。小的齿轮有几个孔。把钢笔或铅笔放入一个孔，然后在较大齿轮（内部有齿）内旋转里面的小齿轮，保持笔与外轮接触，可以画出无数复杂而奇妙的对称图案。

在这个项目中，我们将用Python来创建动画，像万花尺一样绘制曲线。我们的spiro.py程序将用Python和参数方程来描述程序的万花尺齿轮的运动，并绘制曲线（我称之为螺线）。我们可以将完成的画图保存为PNG图像文件，并用命令行选项来指定参数或生成随机螺线。

在这个项目中，我们将学习如何在计算机上绘制螺线。还将学习以下几点：

用turtle模块创建图形；

使用参数方程；

利用数学方程来生成曲线；

用线段来画曲线；

用定时器来生成图形动画；

将图形保存为图像文件。

关于这个项目要注意：我在这个项目中选择了turtle模块用于说明展示，因为它很有趣，但turtle比较慢，如果性能很关键，就不适合用它来创建图形（你对海龟有何期望？）。如果想快速画图，有更好的方法，后面的项目将探索一些可选方案。

2.1　参数方程

在本节中，你将看到用参数方程来画圆的简单例子。参数方程将曲线上点的坐标表示为一个变量的函数，该变量称为参数。参数方程让绘制曲线变得容易，因为只要将参数代入方程就能产生曲线。

注意

如果你现在不想学习这部分数学知识，可以跳到下一部分，讨论针对万花尺项目的方程。

我们开始考虑用半径r来描述一个圆的方程，圆心位于二维平面的原点。x、y坐标满足该方程的所有点构成了圆。

现在，请考虑下面的方程：

x = r cos(θ)　　y = r sin(θ)　　

这些方程是圆的参数表示，其中角θ是参数。这些方程中（X，Y）的任何值，都满足前面描述的圆的方程，X2 + Y2= R2。如果让θ从0变到2π，可以用这些方程来计算圆上对应的x和y坐标。图2-2展示了这种方案。

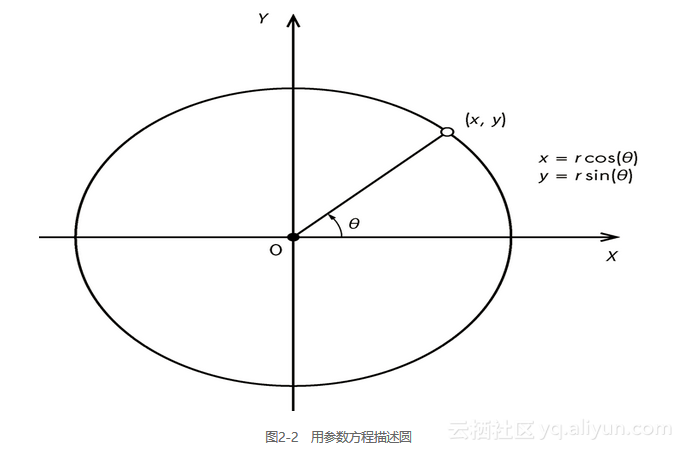
记住，这两个方程适用于圆心在坐标系原点的圆。将圆心转换到点(a, b)，就可以将圆置于xy平面的任何位置。所以更一般的参数方程就变成x = a + r cos(θ)和y = b + r cos(θ)。现在，让我们来看看描述螺线的方程。

2.1.1　万花尺方程

图2-3展示了类似万花尺运动的数学模型。该模型没有齿轮，因为玩具中的齿轮只是为了防止打滑，而在这里不必担心打滑。

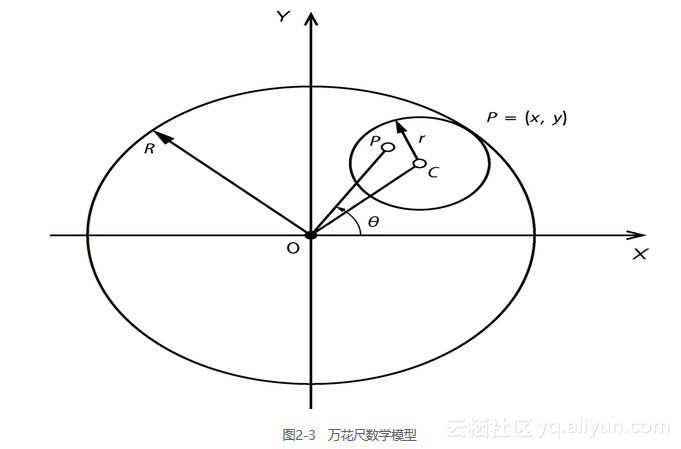
在图2-3中，C是较小的圆的圆心，P是笔尖。较大的圆半径为R，较小的圆半径为r。半径之比表示如下：

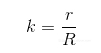
将线段PC与小圆半径r之比作为变量l（l = PC / r），它决定了笔尖离小圆圆心有多远。然后，组合这些变量来表示P的运动，得到如下的参数方程：

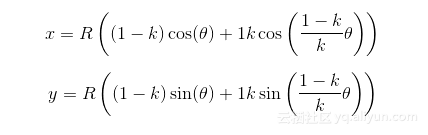
注意

这些曲线称为内旋轮线和外旋轮线。虽然方程可能看起来有点吓人，但推导是非常简单的。如果你想探索其中的数学，请参见维基百科。

图2-4展示了如何用这些方程，基于参数的变化，产生一条曲线。通过改变参数R、r和l，可以产生变化无穷的迷人曲线。

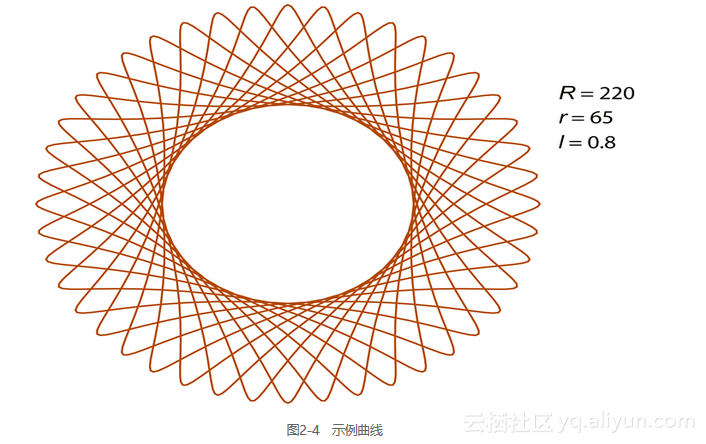
将曲线绘制为一系列点之间的线段。如果这些点足够接近，图看起来就像平滑的曲线。真正玩过万花尺就知道，这取决于使用的参数，万花尺可能需要许多转数来完成。要确定何时停止绘图，就要利用万花尺的周期性（即万花尺图案多久开始重复），研究内外圆的半径之比：

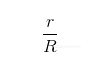
分子分母除以它们的最大公约数（GCD），化简该分数，分子就告诉我们需要多少圈才能完成曲线。例如，在图2-4中，(r, R)的GCD是5。

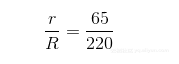
下面是该分数化简后的形式：

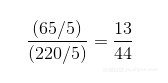
这告诉我们，13圈后，曲线将开始重复。44告诉我们小圆围绕其中心旋转的圈数，它提示了曲线的形状。在图2-4中数一下，会看到图形中花瓣或叶的数目恰好是44！

一旦用简化形式表示了半径比r/R，画出螺线的参数θ范围就是[0，2πr]。这告诉我们何时停止绘制特定的螺线。不知道该角度的结束范围，就会循环不止，不必要地重复该曲线。

2.1.2　海龟画图

我们可以用Python的turtle模块来创建图案。这是一个简单的绘图程序，模型是一只海龟拖着尾巴穿过沙滩，留下图案。turtle模块包括了一些方法，用于设置笔（海龟的尾巴）的位置和颜色，以及其他有用的绘图函数。如你所见，只要少量绘图函数，就可以创建漂亮的螺线。

例如，这个程序用turtle画圆。输入以下代码，保存为drawcircle.py，在Python中运行它：

　import math1 import turtle　 # draw the circle using turtle　 def drawCircleTurtle(x, y, r):　    # move to the start of circle2     turtle.up()3     turtle.setpos(x + r, y)4     turtle.down()　    # draw the circle5    for i in range(0, 365, 5):6         a = math.radians(i)7         turtle.setpos(x + r*math.cos(a), y + r*math.sin(a))8 drawCircleTurtle(100, 100, 50)9 turtle.mainloop()

在1行，从导入turtle模块开始。接下来，定义drawCircleTurtle()方法，它在2行调用up()。这告诉Python提笔。换句话说，让笔离开虚拟的纸，这样移动海龟也不会画图。开始绘图之前，先定位海龟。

在3行，将海龟的位置设置为横轴上的第一个点：(x + r, y)，其中(x，y)是该圆的圆心。现在准备好画图了，所以在4行调用down()。在5行，利用range(0, 365, 5)开始循环，以5为步长递增变量i，从0到360，变量i是角度参数，将传入圆的参数方程，但首先在6行将它从度转为弧度（大多数计算机程序的角度计算需要弧度）。

在7行，利用前面讨论过的参数方程计算圆的坐标，并设置相应的海龟位置，这样就从海龟上一个位置画线到新计算的位置（从技术上讲，产生的是N边多边形，但因为用了很小的角度，N将非常大，多边形看起来像一个圆）。

在8行，调用drawCircleTurtle()来画圆，在9行，调用mainloop()，它保持tkinter窗口打开，让你可以欣赏你画的圆（Tkinter是Python默认的GUI库）。

现在，我们准备好画一些螺线了！